Ak poviem, že tento ("náš") svet je digitalizovaný, tak so mnou budú súhlasiť skoro všetci. Tento „náš“ svet je uložený kdesi na čipoch vo forme jednotiek a núl. Poznáme digitálny záznam obrazu, digitálne vysielanie, digitálne bankovníctvo, digitálne dáta, digitálne..., prosím doplňte si sami.
Tento svet však nie je naším svetom, je odtrhnutý od reality. Reality života, reality prírody, reality bytia. Veľmi rád by som videl mravca budujúceho digitálne mravenisko, či včelu ktorá zbiera digitálne med. Alebo pšenicu, ktorá rastie digitálne.
My ľudia sme sa doslova a do písmena odtrhli od reálneho života a vrhli sa do života digitálneho. Spomeňte si, ako ste svoje deti učili spoznávať, koľko je hodín. „Klasické“ hodiny s ručičkami, malou a veľkou sú typickým príkladom analógového zobrazenia času. Digitálne hodiny vari netreba predstavovať. Digitalizácia naozaj znamenala úžasný pokrok v akejkoľvek ľudskej činnosti, ale je to to „pravé orechové“?
Skúste si predstaviť lietanie – lietadlá, rakety, vrtuľníky. A na druhej strane hmyz, vtáky, netopiere. Jedny lietajú na základe výpočtov digitálne, tie druhé analógovo. Ak ste niekedy pozorovali let akéhokoľvek vtáka, určite vás zaujala jeho neuveriteľná prirodzená elegancia. Je to analógový jav. Nerozumieme mu, nevieme zostrojiť také lietajúce mašinky. Ale s istotou môžeme skonštatovať, že živé lietajúce objekty nemyslia, či nepočítajú digitálne. Digitálne nemyslí ani ľudský mozog. Domnievam sa, že myslí analógovo, ale dokázať to neviem.
Dovolím si uviesť jeden problém, ktorý sa pokúšame riešiť už pomerne dlho. Primárne ho zadal Pierre de Fermat: Vnútri (ostrouhlého) trojuholníka určte taký bod, aby súčet jeho vzdialeností od vrcholov trojuholníka bol čo najmenší. Pre tých, ktorým je toto zadanie príliš cudzie, je úloha možné sformulovať takto: Tri dediny (vrcholy trojuholníka) je treba navzájom spojiť cestami tak, aby sa minulo čo najmenej asfaltu. Úlohu vyriešil Jan Evangelista Torricelli (žiak Galilea Galileiho, ktorý o.i. zostrojil ortuťový (analógový nie digitálny) tlakomer), a preto sa daný bod nazýva Torricelliho bod „T“. Najmenej asfaltu spotrebujeme vtedy ak, z bodu „T“ vidíme myslené tri spojnice medzi dedinami pod rovnakým uhlom - 120 stupňov. Čo je tom také ťažké, poviete si. Nie je to jednoduché, ale dá sa. Poďme ďalej. Tentoraz máme štyri dediny, ktoré sú rozmiestnené vo vrchole štvorca. A znovu máme určiť cestu, ktorá bude spájať všetky štyri obce a na ktorú spotrebujeme najmenej asfaltu. Predpokladajme, že štvorec vo vrcholoch ktorého sú umiestnené jednotlivé dediny, má stranu dlhú 10 km. Väčšina z nás odpovie, že cesty sú to dve navzájom sa pretínajúce uhlopriečky štvorca. Dĺžka ciest bude spolu približne 28,28 km. Nebudem napínať, toto riešenie nie je optimálne. Existujú cesty, ktorých dĺžka je spolu približne 27,32 km. Je to síce len o 3,4% menej, ale je to menej. A dobrý asfalt tiež niečo stojí. Dokonca existujú dve rovnako "dlhé" riešenia. Ako to vieme? Samozrejme niekomu napadlo to spočítať, ale existuje aj „prírodné“ analógové riešenie. Zoberiete dve plexisklové platne a medzi ne vložte (prilepte) štyri rovnako dlhé tenké kolíky, ktoré tvoria vrchol štvorca. Túto sústavu ponorte do vody, do ktorej ste pridali trochu mydla (alebo detergentu na umývanie riadu – napr. jar alebo pur). Nežartujem. Po vytiahnutí z roztoku sa vytvorí (a zobrazí) najkratšia dráha, ktorá je 2,732 (1+ √3) násobkom strany štvorca. Rovnako sa zobrazí aj Torricelliho bod, pravda, ak použijete tri kolíky.
Zázrak? Nie. Rýdza fyzika. Sústava „sa ukladá“ tak, aby jej potenciálna energia dosiahla lokálne minimum. Takto „počíta“ príroda, a ani o tom nevieme. Analógovo. William Miehle publikoval v roku 1958 prácu, kde skúmal minimalizáciu dráh v situácii, keď mal určiť najkratšiu dráhu pri 80 bodoch. Miehle pracoval pre Pentagon a práca sa týkala modelu (ako inak) 62 zbraňových systémov a 18 komunikačných centier. Miehle počítal, až sa mu z kečky parilo. Ako rátal, tak rátal, najmenšia hodnota mu vyšla 105,9 (zvolených jednotiek).
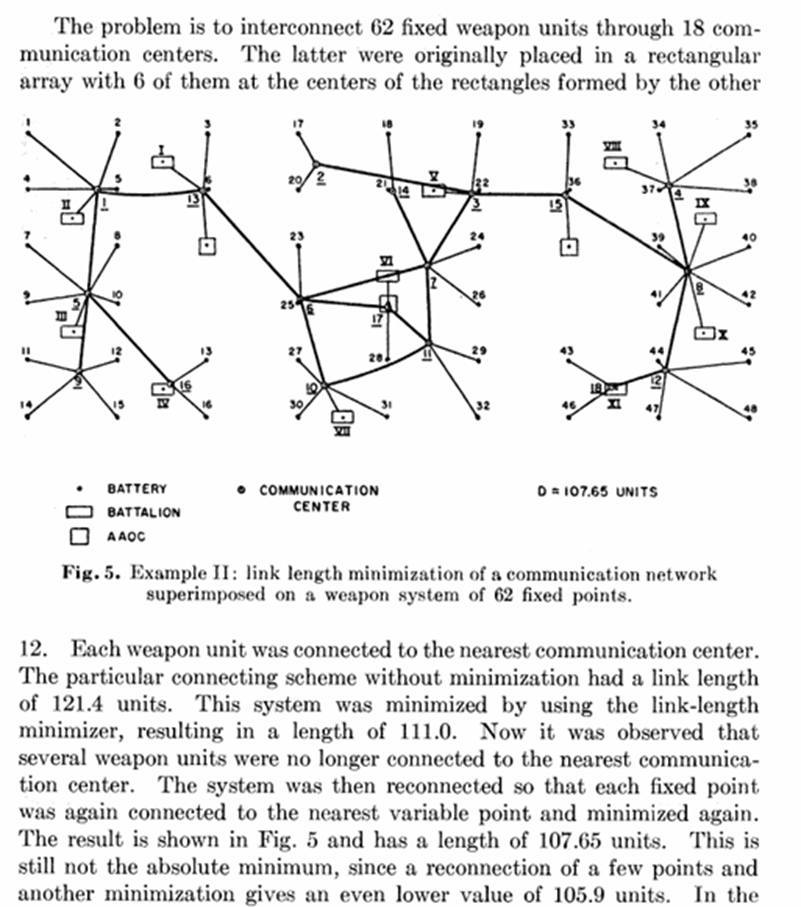
Zostrojil model, ktorý sa skladal z 62 kolíkov. Rovnako dlhé kolíky (62) boli umiestnené medzi dve paralelné platne a podľa danej predlohy. Po ponorení do mydlovej vody a následnom vytiahnutí „vypočítal“, že najkratšia dráha je 68,8 (zvolených jednotiek). To vôbec nevyzeralo zle. Zadávateľ úlohy mohol byť výsostne spokojný. Za málo peňazí (mydlová voda a trochu glycerínu), veru veľa muziky.
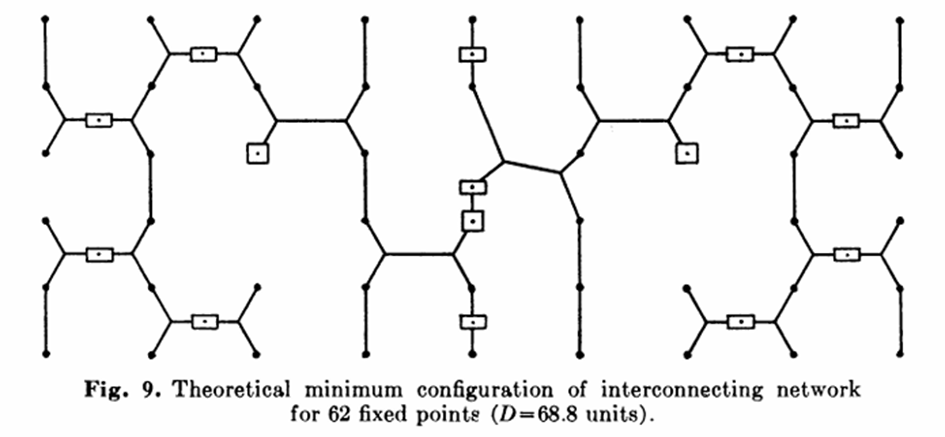
Čo k tomu dodať? Stále mám neodbytný pocit, že sme sa ako odtrhli od koreňov a zapadli do virtuálneho sveta. A to nie je dobré. Stačí CVAK vypínačom a je po ... digitálnosti.
P.S. Obrázky sú z práce William Miehle: Link-Length Minimization in Networks (1958), https://doi.org/10.1287/opre.6.2.232
Publikované: 08.02.2026